5 6 The Quadratic Formula

Slides: nineteen

Download presentation

5. 6 The Quadratic Formula and the Discriminant Algebra 2

five. 6 The Quadratic Formula and the Discriminant Algebra two

Learning Target l Solve equations using the quadratic formula. l Use the discriminant to

Learning Target l Solve equations using the quadratic formula. l Utilise the discriminant to determine the nature of the roots of a quadratic equation.

Derive the quadratic formula from ax 2 + bx + c = 0 a≠

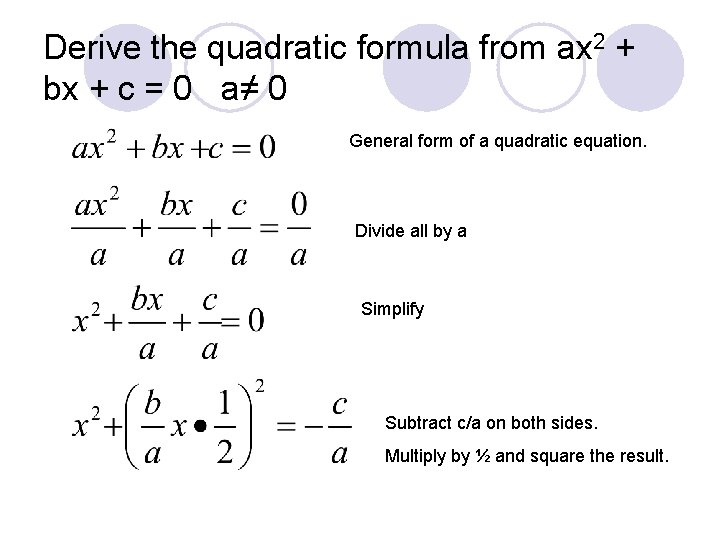
Derive the quadratic formula from ax two + bx + c = 0 a≠ 0 Full general class of a quadratic equation. Divide all by a Simplify Subtract c/a on both sides. Multiply past ½ and square the result.

Derive the quadratic formula from ax 2 + bx + c = 0 a≠

Derive the quadratic formula from ax two + bx + c = 0 a≠ 0 Add the result to both sides. Simplify Multiply past mutual denominator Simplify

Derive the quadratic formula from ax 2 + bx + c = 0 a≠

Derive the quadratic formula from ax ii + bx + c = 0 a≠ 0 Square root both sides Simplify Mutual denominator/subtract from both sides Simplify

Quadratic Formula l The solutions of a quadratic equation of the form ax 2

Quadratic Formula l The solutions of a quadratic equation of the form ax 2 + bx + c with a ≠ 0 are given by this formula: MEMORIZE!!!!

Ex. 1: Solve t 2 – 3 t – 28 = 0 a =

Ex. 1: Solve t two – iii t – 28 = 0 a = 1 b = -three c = -28 There are ii distinct roots—Real and rational.

Ex. 1: Solve t 2 – 3 t – 28 = 0 CHECK: t

Ex. 1: Solve t 2 – 3 t – 28 = 0 CHECK: t 2 – 3 t – 28 = 0 72 – 3(seven) – 28 = 0 49 – 21 – 28 = 0 49 – 49 = 0 CHECK: t two – iii t – 28 = 0 (-four)ii – three(-iv) – 28 = 0 16 + 12 – 28 = 0 28 – 28 = 0

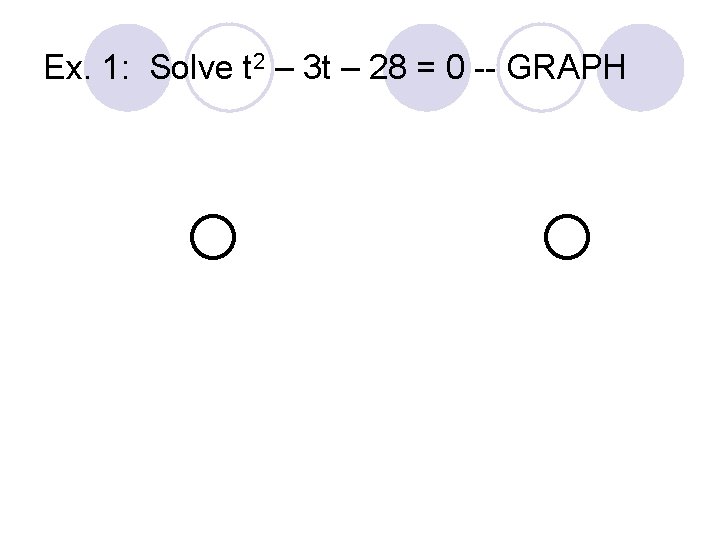
Ex. 1: Solve t 2 – 3 t – 28 = 0 -- GRAPH

Ex. 2: Solve x 2 – 8 x + 16 = 0 a =

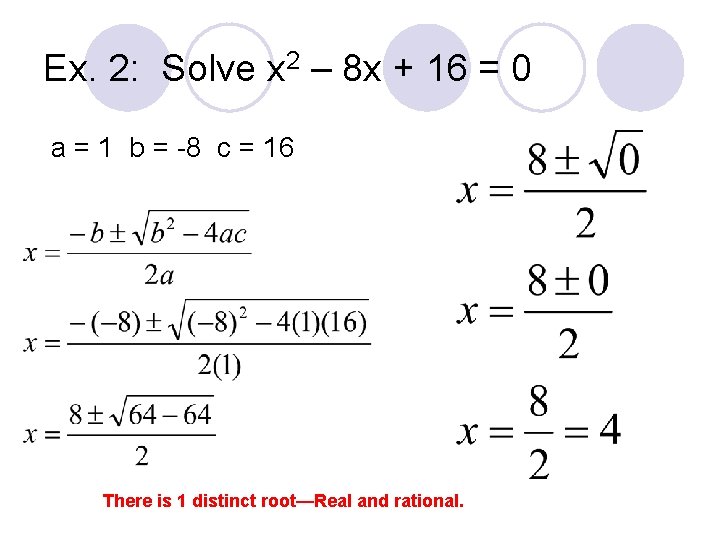
Ex. 2: Solve x 2 – 8 10 + sixteen = 0 a = 1 b = -8 c = 16 There is 1 distinct root—Real and rational.

Ex. 2: Solve x 2 – 8 x + 16 = 0 CHECK: x

Ex. 2: Solve x two – eight x + 16 = 0 Cheque: x ii – viii x + 16 = 0 (4)2 – 8(4) + sixteen = 0 16 – 32 + 16 = 0 32 – 32 = 0 There is one distinct root—Real and rational.

Ex. 2: Solve x 2 – 8 x + 16 = 0 -GRAPH

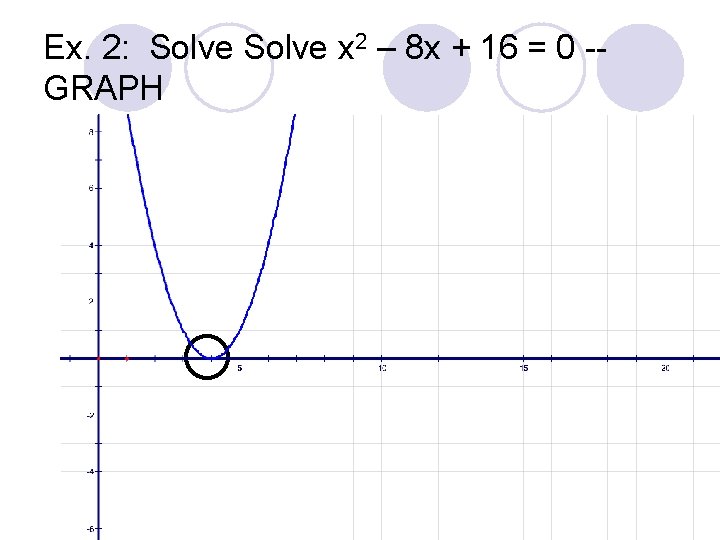
Ex. 2: Solve x 2 – 8 ten + 16 = 0 -GRAPH

Ex. 3: Solve 3 p 2 – 5 p + 9 = 0 a

Ex. 3: Solve 3 p ii – 5 p + ix = 0 a = 3 b = -5 c = nine At that place is 2 imaginary roots.

Ex. 3: Solve 3 p 2 – 5 p + 9 = 0 NOTICE

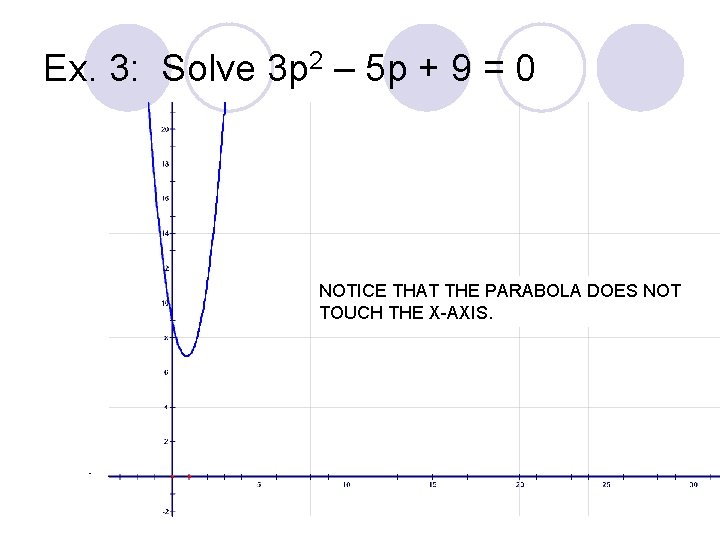
Ex. iii: Solve 3 p 2 – 5 p + 9 = 0 NOTICE THAT THE PARABOLA DOES NOT Bear on THE 10-AXIS.

Note: l These three examples demonstrate a pattern that is useful in determining the

Note: l These 3 examples demonstrate a pattern that is useful in determining the nature of the root of a quadratic equation. In the quadratic formula, the expression under the radical sign, b two – 4 ac is called the discriminant. The discriminant tells the nature of the roots of a quadratic equation.

DISCRIMINANT l The discriminant will tell you about the nature of the roots of

DISCRIMINANT l The discriminant will tell you lot about the nature of the roots of a quadratic equation. Equation t 2 – iii t – 28 = 0 Value of the discriminant Roots b 2 – 4 ac = (-3)2 – 4(i)(-28) = 121 {vii, - four} x 2 – 8 x + xvi = 0 b 2 – 4 air conditioning = {0} Nature of roots 2 real roots ane real root (-eight)two – 4(i)(16) = 0 iii p ii – 5 p + 9 = 0 b 2 – 4 air conditioning = (-5)ii – iv(three)(9) = -83 2 imaginary roots

Ex. 4: Find the value of the discriminant of each equation and then describe

Ex. 4: Find the value of the discriminant of each equation and and then describe the nature of its roots. 2 x two + x – 3 = 0 a = 2 b = 1 c = -3 b ii – 4 ac = (i)two – iv(2)(-3) = 1 + 24 = 25 The value of the discriminant is positive and a perfect square, and then 2 x ii + x – iii = 0 has two real roots and they are rational.

Ex. 5: Find the value of the discriminant of each equation and then describe

Ex. five: Find the value of the discriminant of each equation and then depict the nature of its roots. 10 2 + eight = 0 a=ane b=0 c=8 b ii – 4 ac = (0)ii – 4(1)(8) = 0 – 32 = – 32 The value of the discriminant is negative, so x 2 + eight = 0 has two imaginary roots.

Pair-share l pp. 295 #16 -45 even